Question

If a projectile is fired with an initial velocity of v0 meters per second at an angle α above the horizontal and air resistance is assumed to be negligible, then its position after t seconds is given by the parametric equations

x = (v0 cos α)t y = (v0 sin α)t −1/2gt^2

where g is the acceleration due to gravity (9.8 m/s2). (Round your answers to the nearest whole number.)
(a) If a gun is fired with α = 30° and v0 = 600 m/s. When will the bullet hit the ground?

(a2) How far from the gun will it hit the ground?

(a3)What is the maximum height reached by the bullet?

(b) Find the equation of the parabolic path by eliminating the parameter.

Answer 1

a1) 61 seconds, a2) 31813 meters, a3) 4592 meters, b)
`y = x\cdot \tan 30^(\textdegree) -(1)/(2)\cdot (9.8\,(m)/(s^(2)) )\cdot (x^(2))/([(600\,(m)/(s) )\cdot \cos 30^(\textdegree)]^(2))`

Explanation:

a1) The parametric equations are:

`x = (600\,(m)/(s) \cdot \cos 30^(\textdegree))\cdot t`

`y = (600\,(m)/(s)\cdot \sin 30^(\textdegree) )\cdot t - (1)/(2)\cdot (9.8\,(m)/(s^(2)) )\cdot t^(2)`

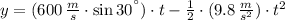
The horizontal distance occurs when
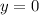`y = 0`. Then:

`-4.9\cdot t^(2) + 300\cdot t = 0`

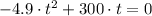
By factoring the expression, roots can be found easily:

`t \cdot (-4.9\cdot t + 300) = 0`

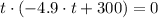
The time needed is:

`t = 61.225\,s`

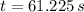
a2) The horizontal distance evaluated at given time is:

`x = 519.615\cdot (61.225\,s)`

`x = 31813.428\,m`

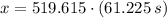
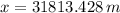
a3) The maximum height reached by occurs when vertical velocity equals to zero. Vertical velocity can be found by deriving the function for vertical position:

`v_(y) = 600\,(m)/(s)\cdot \sin 30^(\textdegree)- (9.8\,(m)/(s^(2)) )\cdot t`

`300 - 9.8\cdot t = 0`

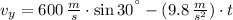
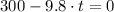
The instant associated with maximum height is:

`t = 30.612\,s`

The maximum height is:

`y = -4.9\cdot (30.612\,s)^(2)+300\cdot (30.612\,s)`

`y = 4591.836\,m`

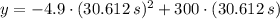
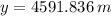
b) The equation is:

`y = x\cdot \tan 30^(\textdegree) -(1)/(2)\cdot (9.8\,(m)/(s^(2)) )\cdot (x^(2))/([(600\,(m)/(s) )\cdot \cos 30^(\textdegree)]^(2))`