Question

If (8, −9) and (6, −3) are the endpoints of the diameter of a circle, what is the equation of the circle?

Answer 1

(x - 7)² + (y + 6)² = 10

Explanation:

The equation of a circle in standard form is

(x - h)² + (y - k)² = r²

where (h, k) are the coordinates of the centre and r is the radius

The centre is at the midpoint of the endpoints of the diameter.

Using the midpoint formula

[
`(1)/(2)`(8 + 6),
`(1)/(2)`(- 9 - 3) ] = (7, - 6) ← coordinates of centre

The radius r is the distance from the centre to either of the endpoints.

Using the distance formula

d = √ (x₂ - x₁ )² + (y₂ - y₁ )²

with (x₁, y₁ ) = (7, - 6) and (x₂, y₂ ) = (6, - 3), then

r =
`√((6-7)^2+(-3+6)^2)`

=
`√((-1)^2+3^2)`

=
`√(1+9)` =
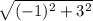
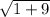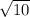`√(10)` ⇒ r² = (
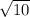`√(10)` )² = 10

Thus equation of circle is

(x - 7)² + (y - (- 6))² = 10, that is

(x - 7)² + (y + 6)² = 10