Question

40 Points ♥ Trigonometry

The area of an isosceles triangle is 100cm².
Calculate the perimeter of the triangle given that one of the angles is π/6 rad.

Answer 1

Case 1: 50.35 cm

Case 2: 56.715 cm

Explanation:

AB = AC;

½ X AH x BC = 100 cm2

=> AH x BH = 100 cm2

=> AH = 100/BH

Case 1: (BAC)=
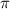`\pi`/6

S = ½ x AB x AC x sin (BAC) = 100 cm2

AB^2 x sin
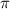`\pi`/6 = 200

=> AB^2 x ½ = 200

=> AB = 20 cm = AC

BC^2 = AB^2 + AC^2 – 2 x AB x AC x cos (BAC) = 202 + 202 – 2 x 20 x 20 x
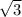`√(3)`/2 = (800 - 400
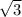`√(3)`) cm

=> BC = 10.35 cm

Perimeter: AB + AC + BC = 20 + 20 + 10.35 = 50.35 cm

Case 2: (ABC) =
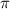`\pi`/6 => (BAC) = 2
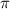`\pi`/3

S = ½ x AB x AC x sin (BAC) = 100 cm2

AB^2 x sin 2
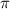`\pi`/3 = 200

=> AB^2 x
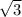`√(3)`/2 = 200

=> AB^2 = 400/
`√(3)`

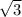
=> AB = AC = 15.197 cm

BC^2 = AB^2 + AC^2 – 2 x AB x AC x cos (BAC) = 400/
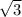`√(3)` + 400/
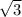`√(3)` – 2 x 400/
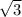`√(3)` x (-1/2) = 692.82 cm

=> BC = 26.321

Perimeter: AB + AC + BC = 15.197 + 15.197 + 26.321 = 56.715 cm