Question

Suppose a 250.0 mL flask is filled with 1.3 mol of I2 and 1.0 mol of HI. The following reaction becomes possible:

H2 (g) +I2 (g) ⇆ 2HI (g)
The equilibrium constant for this reaction is 0.983 at the temperature of the flask.
Calculate the equilibrium molarity of HI. Round your answer to two decimal places.

Answer 1

2.27 M

Step-by-step explanation:

Given that :

volume = 250.0 mL = 0.250 L

Number of moles of
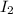`I_2` = 1.3 mol

Number of moles of
`HI` = 1.0 mole

Initial concentration of
`I_2` =
`(numbers of mole)/(volume)`

=
`(1.3)/(0.250)`

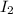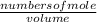
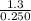
= 5.20 M

Initial concentration of
`HI` =
`(numbers of mole)/(volume)`

=
`(1.0)/(0.250)`

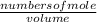
= 4.0 M

Equation of the reaction is represented as:

`H_2}_((g)) + I_2_((g))----->2HI_((g))`

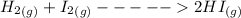
The I.C.E Table is as follows:

`H_2}_((g))` +
`I_2_((g))` ----->
`2HI_((g))`

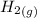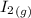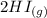
Initial(M) 0.0 5.20 4.0

Change +x +x - 2x

Equilibrium(M) x 5.20+x 4 - 2x

`K = ([HI]^2)/([H_2][I_2])`

`K = ([4-2x]^2)/([x][5.20+x])` where K = 0.983

`0.983 = ((4-2x)^2)/((5.20x+x^2))`

`0.983(5.20x+x^2) = (4-2x)^2`

`5.1116x + 0.983x^2=16-16x+4x^2`

`5.1116x +16x + 0.983x^2 -4x^2 -16 =0`

`21.1116x - 3.017x^2 -16 =0`

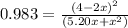
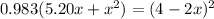
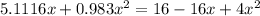
multiplying through by (-) and rearranging in the order of quadratic equation; we have:

`3.017x^2 -21.1116x +16`

`x^2 - 6.9975+5.30 =0`

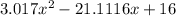
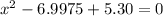
using the quadratic formula:

=
`(-b \pm√(b^2-4ac) )/(2a)`

=
`(-(-6.9975) \pm√((-6.9975)^2-4(1)(5.3)) )/(2(1))`

=
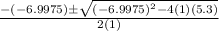
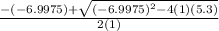`(-(-6.9975) + √((-6.9975)^2-4(1)(5.3)) )/(2(1))` OR
`(-(-6.9975) - √((-6.9975)^2-4(1)(5.3)) )/(2(1))`

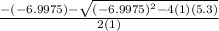
= 6.133 OR 0.864

since 6.133 is greater than K value then it is void, so we go by the lesser value which is 0.864

so x = 0.864 M

The equilibrium molarity of HI = (4.0- 2x)

= 4.0 - 2(0.864)

= 4.0 - 1.728

= 2.272 M

= 2.27 M to two decimal places