Question

Which is the solution set of the inequality
-15y+9<-36

Answer 1

`-15y+9<-36\quad :\quad \begin{bmatrix}\mathrm{Solution:}\:&\:y>3\:\\ \:\mathrm{Interval\:Notation:}&\:\left(3,\:\infty \:\right)\end{bmatrix}`

Therefore, the first choice is correct.

The graph of the inequality is also attached below.

Explanation:

Considering the inequality

`-15y+9<-36`

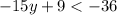
solving

`-15y+9<-36`

`\mathrm{Subtract\:}9\mathrm{\:from\:both\:sides}`

`-15y+9-9<-36-9`

`-15y<-45`

`\mathrm{Multiply\:both\:sides\:by\:-1\:\left(reverse\:the\:inequality\right)}`

`\left(-15y\right)\left(-1\right)>\left(-45\right)\left(-1\right)`

`15y>45`

`\mathrm{Divide\:both\:sides\:by\:}15`

`(15y)/(15)>(45)/(15)`

`y>3`

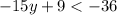
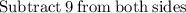
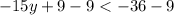
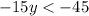
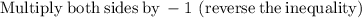
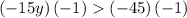
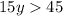
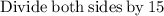
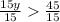
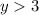
In other words,

`-15y+9<-36\quad :\quad \begin{bmatrix}\mathrm{Solution:}\:&\:y>3\:\\ \:\mathrm{Interval\:Notation:}&\:\left(3,\:\infty \:\right)\end{bmatrix}`

Therefore, the first choice is correct.

The graph of the inequality is also attached below.