Question

An equilibrium mixture of PCl 5 ( g ) , PCl 3 ( g ) , and Cl 2 ( g ) has partial pressures of 217.0 Torr, 13.2 Torr, and 13.2 Torr, respectively. A quantity of Cl 2 ( g ) is injected into the mixture, and the total pressure jumps to 263.0 Torr at the moment of mixing. The system then re-equilibrates. The chemical equation for this reaction is PCl 3 ( g ) + Cl 2 ( g ) − ⇀ ↽ − PCl 5 ( g ) Calculate the new partial pressures, P , after equilibrium is reestablished.

Answer 1

`p_(PCl_5)=223.407torr\\p_(PCl_3)=6.796torr\\p_(Cl_2)=26.396torr`

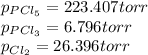
Step-by-step explanation:

Hello,

In this case, the undergoing chemical reaction is:

`PCl_3(g)+Cl_2(g)\leftrightarrow PCl_5(g)`

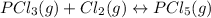
And the equilibrium constant at the reaction's temperature is:

`Kp=(p_(PCl_5))/(p_(PCl_3)p_(Cl_2))=(217.0torr)/((13.2torr)(13.2torr)) =1.2454`

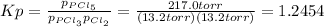
Now, even when chlorine is added, such pressure equilibrium constant does not change, therefore, since the initial total pressure is:

`p_(T0)=217.0torr+13.2torr+13.2torr=243.4torr`

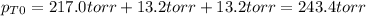
The new pressures, due to the change
`x` owing to the chlorine's addition, turn out:

`p_(PCl_5)=p_(PCl_5)^0+x\\p_(PCl_3)=p_(PCl_3)^0-x\\p_(Cl_2)=p_(Cl_2)^0+p_(Cl_2)^(added)-x`

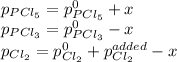
Therefore, the added chlorine is:

`p_(Cl_2)^(added)=263torr-243.4torr=19.6torr`

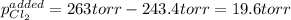
Thus, the new partial pressures are found via the law of mass action in terms of the change
`x` as follows:

`1.2454=((217+x))/((32.8-x)(13.2-x))`

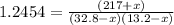
Solving for
`x` one obtains:

`x=6.404torr`

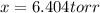
Finally, the new partial pressures result:

`p_(PCl_5)=217torr+6.404torr=223.407torr\\p_(PCl_3)=13.2torr-6.404torr=6.796torr\\p_(Cl_2)=32.8torr-6.404torr=26.396torr`

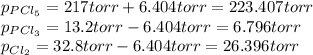
Best regards.