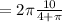Question

You have a wire that is 20 cm long. You wish to cut it into two pieces. One piece will be bent into the shape of a square. The other piece will be bent into the shape of a circle. Let A represent the total area of the square and the circle. What is the circumference of the circle when A is a minimum

Answer 1

Therefore the circumference of the circle is
`=(20\pi)/(4+\pi)`

Explanation:

Let the side of the square be s

and the radius of the circle be r

The perimeter of the square is = 4s

The circumference of the circle is =2πr

Given that the length of the wire is 20 cm.

According to the problem,

4s + 2πr =20

⇒2s+πr =10

`\Rightarrow s=(10-\pi r)/(2)`

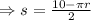
The area of the circle is = πr²

The area of the square is = s²

A represent the total area of the square and circle.

A=πr²+s²

Putting the value of s

`A=\pi r^2+ ((10-\pi r)/(2))^2`

`\Rightarrow A= \pi r^2+((10)/(2))^2-2.(10)/(2).(\pi r)/(2)+ ((\pi r)/(2))^2`

`\Rightarrow A=\pi r^2 +25-5 \pi r +(\pi^2r^2)/(4)`

`\Rightarrow A=\pi r^2(4+\pi)/(4) -5\pi r +25`

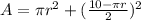
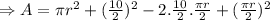
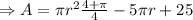
For maximum or minimum
`(dA)/(dr)=0`

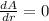
Differentiating with respect to r

`(dA)/(dr)= (2\pi r(4+\pi))/(4) -5\pi`

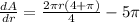
Again differentiating with respect to r

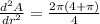`(d^2A)/(dr^2)=(2\pi (4+\pi))/(4)` > 0

For maximum or minimum

`(dA)/(dr)=0`

`\Rightarrow (2\pi r(4+\pi))/(4) -5\pi=0`

`\Rightarrow r = (10\pi )/(\pi(4+\pi))`

`\Rightarrow r=(10)/(4+\pi)`

`(d^2A)/(dr^2)|_{ r=(10)/(4+\pi)}=(2\pi (4+\pi))/(4)>0`

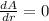
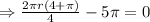
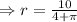
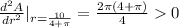
Therefore at
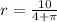`r=(10)/(4+\pi)` , A is minimum.

Therefore the circumference of the circle is

`=2 \pi (10)/(4+\pi)`

`=(20\pi)/(4+\pi)`