Answer:
The value of rate of decrease of volume = - 3600
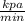
Explanation:
According to Boyle's law P V = C ------- (1)
Pressure ( P ) = 100 k pa = 10
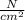
Volume ( V ) = 900

Put these values in equation ( 1 ) we get,
⇒ C = 10 × 900 = 9000 N-cm = 90 N-m
Differentiate Equation ( 1 ) with respect to time we get,
⇒ V
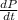 + P
+ P
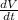 = 0
= 0
⇒ V
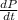 = - P
= - P
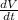
⇒
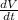 = -
= -
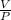
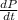 ---------- (2)
---------- (2)
This equation gives the rate of decrease of volume.
Given that Rate of increase of pressure =
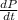 = 40
= 40
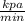
C = 90 N-m
P =
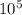 pa = 10
pa = 10
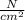
V = 900

Put all the above values in equation 2 we get,
⇒
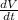 = -
= -
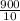 × 40
× 40
⇒
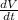 = - 3600
= - 3600
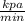
This is the value of rate of decrease of volume.