Option A: 25 units is the distance between the points
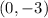 and
and
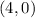
Step-by-step explanation:
Given that the two coordinates
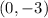 and
and
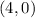
We need to determine the distance between these two points.
The distance between the two points can be determined using the distance formula,
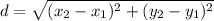
Substituting the coordinates in the formula, we get,
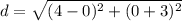
Simplifying the terms within the bracket, we get,
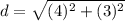
Squaring the terms, we get,
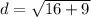
Adding, we get,
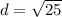
Simplifying, we have,
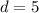
Thus, the distance between the two points is 5 units.
Therefore, Option A is the correct answer.