Question

The activation energy of a certain reaction is 37.4 kJ/mol . At 25 ∘C , the rate constant is 0.0160s−1 . At what temperature in degrees Celsius would this reaction go twice as fast?

Answer 1

The correct answer is 312.3 K

Step-by-step explanation:

In order to solve the problem, we use the modified Arrhenius equation which comprises two rate constants (k) and two temperatures (T):

`ln ((k_(2) )/(k_(1) ) ) = (Ea)/(R) ((1)/(T_(1))- (1)/(T_(2) ) )`

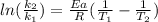
Where Ea is the activation energy (37.4 kJ/mol= 37400 J/mol), R is the gases constant (8.31 J/K.mol), k₁ and k₂ are the rate constant. We know k₁ (0.0160 s⁻¹) and from the problem, k₂ is twice k₁, so k₂= 2 x k₁= 2 x 0.0160 s⁻¹= 0.032 s⁻¹). Finally, T₁= 25ºC + 273 = 298 K. We introduce the data in the equation and calculate T₂:

`ln ((0.032s^(-1) )/(0.0160s^(-1) ) )= ((37400 J/mol)/(8.31 J/mol.K)) ((1)/(298 K) - (1)/(T_(2) ) )`

`ln (2) = (4,500.6 K) ( ((1)/(298 K))-((1)/(T_(2) ) ))`

`T_(2)= (1)/(((1)/(298K))-((ln2)/(4,500.6K)) )`

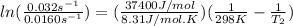
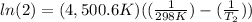
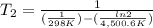
T₂= 312.33 K