Answer: f(x) = (x-4)^2+8 for vertex form.
Explanation:
Given Quadratic Function f(x) = x^2-8x+24
As you know, the standard form is y = ax^2+bx+c where a,b and c are part of real numbers. and a musn't be 0
For vertex form, a(x-h)^2+k and (h,k) is vertex of graph.
We are going to change the standard form to vertex form so we can graph it easily.
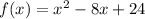
 By completing the square.
By completing the square.

Now we know vertex and that is (4,8)
For Axis of Symmetry = h
Then draw the graph.
From the graph, vertex is not on x-axis, meaning that there are no common points (The equation has a complex solution/answer.)