Question

The human ear canal is about 2.9 cm long and can be regarded as a tube open at one end and closed at the eardrum. What is the fundamental frequency around which we would expect hearing to be most sensitive? Assume the speed of sound in air to be 339 m/s. Answer in units of kHz.

Answer 1

The frequency of the human ear canal is 2.92 kHz.

Explanation:

As the ear canal is like a tube with open at one end, the wavelength of sound passing through this tube will propagate 4 times its length of the tube. So wavelength of the sound wave will be equal to four times the length of the tube. Then the frequency can be easily determined by finding the ratio of velocity of sound to wavelength. As the velocity of sound is given as 339 m/s, then the wavelength of the sound wave propagating through the ear canal is

Wavelength=4*Length of the ear canal

As length of the ear canal is given as 2.9 cm, it should be converted into meter as follows:

`wavelength = 4*2.9*10^(-2) =0.116`

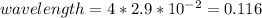
Then the frequency is determined as

f=c/λ=339/0.116=2922 Hz=2.92 kHz.

So, the frequency of the human ear canal is 2.92 kHz.