Question

A normal population has a mean of 62 and a standard deviation of 12. You select a random sample of 25. Compute the probability the sample mean is (Round z values to 2 decimal places and final answers to 4 decimal places): (a) Greater than 64.

Answer 1

(a) Probability that the sample mean is Greater than 64 is 0.2033 .

Explanation:

We are given that a normal population has a mean of 62 and a standard deviation of 12 and we select a random sample of 25.

Let X bar = sample mean

The z score probability distribution for sample mean is ;

Z =
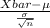`(Xbar-\mu)/((\sigma)/(√(n) ) )` ~ N(0,1)

where,
`\mu` = population mean = 62

`\sigma` = population standard deviation = 12

n = random sample = 25

So, probability that the sample mean is Greater than 64 = P(X bar > 64)

P(X bar > 64) = P(
`(Xbar-\mu)/((\sigma)/(√(n) ) )` <
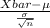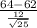`(64-62)/((12)/(√(25) ) )` ) = P(Z > 0.83) = 1 - P(Z <= 0.83)

= 1 - 0.79673 = 0.2033 .