2 Answers

Brig · Answer 1 · 2021-06-25T01:37:34+0000

Answer:

x = 19, 17

Explanation:

(x-18)(x-18)=1

x^2 - 36x + 324=1

x^2 - 36x = -323

x^2 - 36x + 323 = 1

(x-19)(x-17) = 0

x = 19, 17

Guido Celada · Answer 2 · 2021-06-28T05:03:32+0000

Answer: x = 17,19

Explanation:

Method 1: Solve by Equations

The most common method, so...

(x-18)^2=1

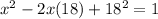
x^2-2x(18)+18^2=1

x^2-36x+324=1

Move 1 to the left.

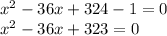
$x^2-36x+324-1=0\\x^2-36x+323=0$

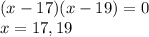
$(x-17)(x-19)=0\\x=17,19$

The value of x are 17 and 19.

I don't recommend this method since you might be bad at graphing (You must be perfect at graphing)

So given
(x-18)^2=1

Move 1 to the left

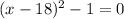
(x-18)^2-1=0

Change 0 to y

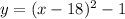y=(x-18)^2-1 The vertex is at (18,-1)

Draw the graph (Parabola)

When you finish drawing the graph, x-intercepts should be around 17 and 19

x-intercepts are the value of x so if x-intercepts are at (17,0) and (19,0) then the value of x are both 17 and 19