Answer:
The final speed of the system is 21 cm/s.
Step-by-step explanation:
Given:
Mass of the cart (M) = 236 g
Initial velocity of the cart (U) = 26.9 cm/s
Mass of the clay (m) = 66.1 g
Initial velocity of the clay (u) = 0 cm/s (At rest initially)
Let the final velocity of the system be 'v'.
Now, total initial momentum is given as:
Initial momentum = Initial momentum of cart + Initial momentum of clay
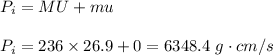
Final momentum of the system is given as:
Final momentum = Total mass × Final velocity
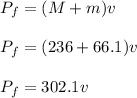
Now, from conservation of total momentum, final momentum is equal to initial momentum. So,
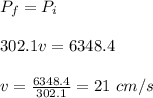
Therefore, the final speed of the system is 21 cm/s.