Question

A car travels at a steady 40.0 m/s around a horizontal curve of radius 200 m. What is the minimumcoefficient of static friction between the road and the car's tires that will allow the car to travel atthis speed without sliding?

a. 1.23
b. 0.662
c. 0.816
d. 0.952
e. 0.736

Answer 1

c. 0.816

Step-by-step explanation:

Let the mass of car be 'm' and coefficient of static friction be 'μ'.

Given:

Speed of the car (v) = 40.0 m/s

Radius of the curve (R) = 200 m

As the car is making a circular turn, the force acting on it is centripetal force which is given as:

Centripetal force is,
`F_c=(mv^2)/(R)`

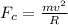
The frictional force is given as:

Friction = Normal force × Coefficient of static friction

`f=\mu N`

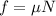
As there is no vertical motion, therefore,
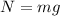`N=mg`. So,

`f=\mu mg`

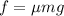
Now, the centripetal force is provided by the frictional force. Therefore,

Frictional force = Centripetal force

`f=F_c\\\\\mu mg=(mv^2)/(R)\\\\\mu=(v^2)/(Rg)`

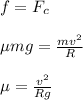
Plug in the given values and solve for 'μ'. This gives,

`\mu = ((40\ m/s)^2)/(200\ m* 9.8\ m/s^2)\\\\\mu=(1600\ m^2/s^2)/(1960\ m^2/s^2)\\\\\mu=0.816`

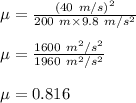
Therefore, option (c) is correct.