Answer:
0.623
Explanation:
We have to find the probability that a diagnosis is correct given that confidence in the correctness of diagnosis is high i.e.P(C/H)=?
Using Bayes' theorem the probability can be computed as
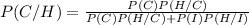
We are given that
P(C) = 0.262 , P(H/C) = 0.344 , P(I) = 0.738 and P(H/I) = 0.074.
So,
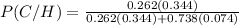
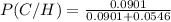
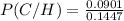
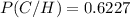
P(C/H)=0.623 (rounded to three decimal places).
Thus, the probability that a diagnosis is correct given that confidence in the correctness of diagnosis is high is 0.623.