Question

The Environmental Protection Agency (EPA) has contracted with your company for equipment to monitor water quality for several lakes in your water district. A total of 10 devices will be used. Assume that each device has a probability of 0.01 of failure during the course of the monitoring period. What is the probability that none of your devices fail

Answer 1

The probability that none of the devices fails happens when x = 0.

P(none fail) = 1(0.01)^(0)•(1 - 0.01)^(10)

P(none fail) = (0.01)^0•(0.99)^(10)

P(none fail) = 0.90438

Answer 2

Probability that none of your devices fail is 0.9044.

Explanation:

We are given that the Environmental Protection Agency (EPA) has contracted with your company for equipment to monitor water quality for several lakes in your water district. A total of 10 devices will be used. Assume that each device has a probability of 0.01 of failure during the course of the monitoring period.

The above situation can be represented through Binomial distribution;

`P(X=r) = \binom{n}{r}p^(r) (1-p)^(n-r) ; x = 0,1,2,3,.....`

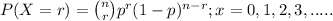
where, n = number of trials (samples) taken = 10 devices

r = number of success = none fail

p = probability of success which is probability of failure during the

course of the monitoring period, i.e; 0.01.

LET X = No. of failures

So, it means X ~
`Binom(n=10, p=0.01)`

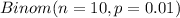
Now, Probability that none of your devices fail is given by = P(X = 0)

P(X = 0) =
`\binom{10}{0} * 0.01^(0) * (1-0.01)^(10-0)`

=
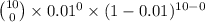
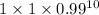`1 * 1 * 0.99^(10)` = 0.9044

Hence, the probability that none of your devices fail is 0.9044.