Area of the polygon defined by the given points is 62.5 sq units
Explanation:
Step 1 :
Let P be the point (-5,0) Q = (0,-5), R = (-15,-20) and S = (20,-15)
We have to to find the area of the polygon PQRS
Step 2 :
The area of polygon given the vertices (x
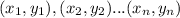 is given by
is given by
Area = mod (
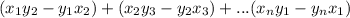 ) ÷ 2
) ÷ 2
Where
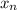 is the vertex n's x coordinate ,
is the vertex n's x coordinate ,
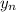 is the vertex n's y coordinate
is the vertex n's y coordinate
Substituting the corresponding values ,
Area of PQRS = mod ( (25 - 0)+ (0-75) +(300-300) +( 0-75) ) ÷ 2
= mod (25-75+0-75) ÷ 2
= mod (-125) ÷ 2 = 125 ÷ 2 = 62.5 sq units
Step 3 :
Answer :
Area of the polygon defined by the given points is 62.5 sq units