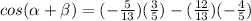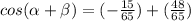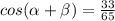Question

Angle α lies in quadrant II , and tanα=−125 . Angle β lies in quadrant IV , and cosβ=35 .

What is the exact value of cos(α−β) ?

Answer 1

`cos(\alpha+\beta)=(33)/(65)`

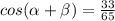
Explanation:

step 1

Find cos α

we know that

`tan^2(\alpha)+1=sec^2(\alpha)`

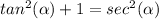
we have

`tan(\alpha)=-(12)/(5)`

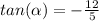
substitute

`(-(12)/(5))^2+1=sec^2(\alpha)`

`sec^2(\alpha)=(144)/(25)+1`

`sec^2(\alpha)=(169)/(25)`

`sec(\alpha)=\pm(13)/(5)`

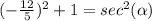
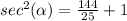
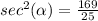
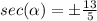
Remember that Angle α lies in quadrant II

so

sec α is negative

`sec(\alpha)=-(13)/(5)`

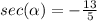
Find the value of cos α

`cos)\alpha)=(1)/(sec(\alpha))`

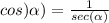
so

`cos(\alpha)=-(5)/(13)`

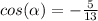
step 2

Find sin α

we know that

`tan(\alpha)=(sin(\alpha))/(cos(\alpha))`

`sin(\alpha)=tan(\alpha)cos(\alpha)`

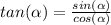
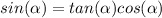
we have

`tan(\alpha)=-(12)/(5)`

`cos(\alpha)=-(5)/(13)`

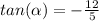
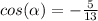
substitute

`sin(\alpha)=(-(12)/(5))(-(5)/(13))`

`sin(\alpha)=(12)/(13)`

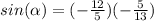
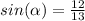
step 3

Find sin β

we know that

`sin^2(\beta)+cos^2(\beta)=1`

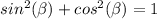
we have

`cos(\beta)=(3)/(5)`

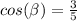
substitute

`sin^2(\beta)+((3)/(5))^2=1`

`sin^2(\beta)=1-((3)/(5))^2`

`sin^2(\beta)=1-(9)/(25)`

`sin^2(\beta)=(16)/(25)`

`sin(\beta)=\pm(4)/(5)`

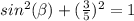
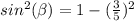
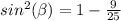
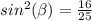
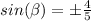
Remember that

Angle β lies in quadrant IV

so

sin β is negative

`sin(\beta)=-(4)/(5)`

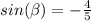
step 4

Find cos(α−β)

we know that

`cos(\alpha+\beta)=cos(\alpha)cos(\beta)-sin(\alpha)sin(\beta)`

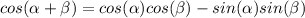
we have

`cos(\alpha)=-(5)/(13)`

`cos(\beta)=(3)/(5)`

`sin(\alpha)=(12)/(13)`

`sin(\beta)=-(4)/(5)`

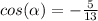
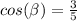
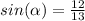
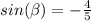
substitute the given values

`cos(\alpha+\beta)=(-(5)/(13))((3)/(5))-((12)/(13))(-(4)/(5))`

`cos(\alpha+\beta)=(-(15)/(65))+((48)/(65))`

`cos(\alpha+\beta)=(33)/(65)`