Question

As part of her architecture project. Amira built a replica of the Dome of the Rock. It is an octagonal prism with a hemispherical dome situated in the middle of the ceiling. Each wall is 9 inches wide and 5.5 inches tall. The hemisphere has a radius of 10 inches. To the nearest square inch how much paint does Amira need to paint her replica? (Note: the surface area of a sphere is 4πr², and Amira does not need to paint the floor of her replica)

Answer 1

1492.21 square in.

Explanation:

The Dome of Rock replica is basically an octagonal prism with a hemisphere on top (middle).

We need to find the outer surface area of this. This will be our answer.

We will find surface area of "octagonal prism" MINUS the bottom part of the hemisphere (since it is in middle of top part of octagonal prism).

Also, we will find surface area of hemisphere (disregard the bottom, that won't be painted).

Now,

Surface Area of Octagonal Prism =
`8bh+4(1+√(2))b^2`

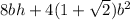
Where "b" is the base length (9 inches), and h is the height of the wall (5.5 inches)

So, the surface area would be:

SA =
`8bh+4(1+√(2))b^2=8(9)(5.5)+4(1+√(2))(9)^2=1178.21`

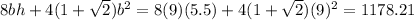
Now, the bottom of hemisphere is the circle with area
`\pi r^2`

So, area of that circle is =
`\pi(10)^2=100\pi = 314`

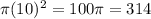
We subtract this to get:

SA of octagonal prism = 1178.21 - 314 = 864.21

Now, area of the hemisphere (without bottom). THe formula is:

SA of dome =
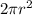`2\pi r^2`, where r is radius (10 cm)

So,

SA of dome =
`2\pi r^2 = 2\pi (10)^2 = 2\pi (100) = 200\pi = 628`

Hence, total surface area of Dome of Rock to be painted is:

TSA = 864.21 + 628 = 1492.21 square in.