Answer:
The dimension of the open rectangular box is
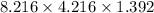 .
.
The volume of the box is 8.217 cubic inches.
Explanation:
Given : The open rectangular box of maximum volume that can be made from a sheet of cardboard 11 in. by 7 in. by cutting congruent squares from the corners and folding up the sides.
To find : The dimensions and the volume of the open rectangular box ?
Solution :
Let the height be 'x'.
The length of the box is '11-2x'.
The breadth of the box is '7-2x'.
The volume of the box is

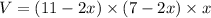
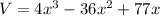
Derivate w.r.t x,
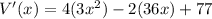
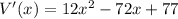
The critical point when V'(x)=0
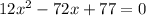
Solve by quadratic formula,
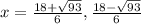
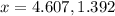
Derivate again w.r.t x,
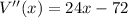
Now,
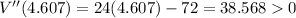 (+ve)
(+ve)
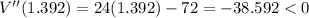 (-ve)
(-ve)
So, there is maximum at x=1.392.
The length of the box is
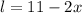
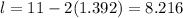
The breadth of the box is
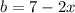
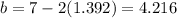
The height of the box is h=1.392.
The dimension of the open rectangular box is
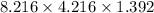 .
.
The volume of the box is

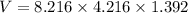
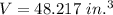
The volume of the box is 8.217 cubic inches.