The given question is incomplete. The complete question is as follows.
A basic solution contains the iodide and phosphate ions that are to be separated via selective precipitation. the i– concentration, which is 9.00×10-5 m, is 10,000 times less than that of the
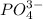 ion at 0.900 m . a solution containing the silver(i) ion is slowly added. answer the questions below. ksp of agi is 8.30×10-17 and of
ion at 0.900 m . a solution containing the silver(i) ion is slowly added. answer the questions below. ksp of agi is 8.30×10-17 and of
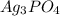 ,
,
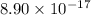 .
.
Calculate the minimum
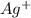 concentration required to cause precipitation of AgI.
concentration required to cause precipitation of AgI.
Step-by-step explanation:
It is known that at the stage of precipitation, the
 is equal to the ionic product.
is equal to the ionic product.
Therefore, expression for
 for
for
 is as follows.
is as follows.
![K_(sp) = [Ag^(+)][I^(-)]](https://img.qammunity.org/2021/formulas/chemistry/high-school/7b8mg4n894luc3s209r9dd0ln2kwkaspwi.png)
In the given case,
![[I^(-)] = 7.7 * 10^(-5)](https://img.qammunity.org/2021/formulas/chemistry/high-school/s9unc706c8fmrh05i65nrcgpdfwwq34zf1.png)
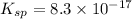
Hence,
![[Ag^(+)] = (k_(sp))/(I^(-))](https://img.qammunity.org/2021/formulas/chemistry/high-school/3kd3p9j99typelmb6k29uueinxbdh78ihb.png)
=
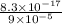
=
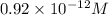
Now, for
 the expression for
the expression for
 will be as follows.
will be as follows.
![K_(sp) = [Ag^(+)]^(3)[PO^(3-)_(4)]](https://img.qammunity.org/2021/formulas/chemistry/high-school/zp9twl7ooh2jh4ygh4xfirxtu1e2kr4ae1.png)
or,
![[Ag^(+)] = ((K_(sp))/([PO^(3-)_(4)]))^{(1)/(3)}](https://img.qammunity.org/2021/formulas/chemistry/high-school/1lvawurqhjnvq599b3q4btl55e5ffhzzg2.png)
=
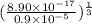
=
 M
M