Answer:
Probability of a bulb lasting for at most 560 hours = 0.8413 .
Explanation:
We are given that the life of light bulbs is distributed normally. The variance of the lifetime is 400 and the mean lifetime of a bulb is 540 hours.
Let X = life of light bulbs
So, X ~ N(
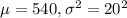 )
)
The z score probability distribution is given by;
Z =
 ~ N(0,1)
~ N(0,1)
where,
 = population mean and
= population mean and
 = standard deviation
= standard deviation
So, Probability of a bulb lasting for at most 560 hours = P(X <= 560 hours)
P(X <= 560) = P(
 <=
<=
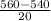 ) = P(Z <= 1) = 0.8413
) = P(Z <= 1) = 0.8413
Therefore, probability of a bulb lasting for at most 560 hours is 0.8413 .