Question

A wooden block with mass 1.60 kg is placed against a compressed spring at the bottom of a slope inclined at an angle of 30.0° (point A). When the spring is released, it projects the block up the incline. At point B, a distance of 6.55 m up the incline from A, the block is moving up the incline at a speed of 7.50 m/s and is no longer in contact with the spring. The coefficient of kinetic friction between the block and incline is
`\mu_k` = 0.50. The mass of the spring is negligible.

Calculate the amount of potential energy that was initially stored in the spring. Take free fall acceleration to be 9.80 m/s².

Answer 1

The amount of potential energy that was initially stored in the spring is 88.8 J.

Step-by-step explanation:

Given that,

Mass of block = 1.60 kg

Angle = 30.0°

Distance = 6.55 m

Speed = 7.50 m/s

Coefficient of kinetic friction = 0.50

We need to calculate the amount of potential energy

Using formula of conservation of energy between point A and B

`U_(A)+k_(A)+w_(A)=U_(B)+k_(B)`

`U_(A)+0-fd=mgy+(1)/(2)mv^2`

`U_(A)=\mu mg\cos\theta* d+mg h\sin\theta+(1)/(2)mv^2`

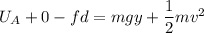
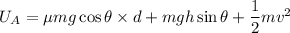
Put the value into the formula

`U_(A)=0.50*1.60*9.8\cos30*6.55+1.60*9.8*6.55\sin30+(1)/(2)*1.60*(7.50)^2`

`U_(A)=88.8\ J`

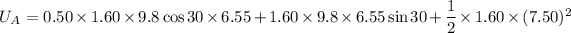
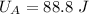
Hence, The amount of potential energy that was initially stored in the spring is 88.8 J.