Answer:
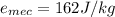
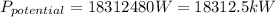
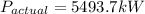
Step-by-step explanation:
Given data
Diameter d=80m
Speed v=18 m/s
Efficiency n=30%
Air density p=1.25 kg/m³
For Mechanical energy of air per unit mass
The power potential of wind per unit mass could be defined as follow:
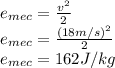
For Power generation potential
The generation potential of turbine will determined from the available kinetic energy of air:
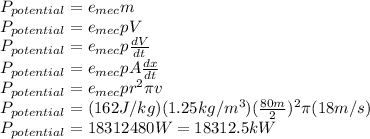
For Actual power
The actual power generation could be defined as follow as:
