Here is the full question
A rocket is launched from a tower. The height of the rocket, y in feet, is related to the time after launch, x in seconds, by the given equation. Using this equation, find the time that the rocket will hit the ground, to the nearest 100th of second.
Equation:
y=-16x^2+153x+98
Answer:
10.2 seconds
Explanation:
Given equation :
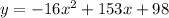 shown the expression of a quadratic equation
shown the expression of a quadratic equation
Let y =0
∴
0 =
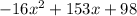
where;
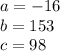
Using the quadratic formula:
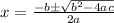
replacing it with our values; we have:
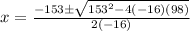
 OR
OR
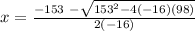
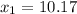 OR
OR

Hence, we go by the positive value since, is the time that the rocket will hit the ground.
x= 10.17
x = ≅ 10.2 seconds
Therefore, the rocket will hit the ground, to the nearest 100th of second. = 10.2 seconds