Question

59% of the working population attended college. If a person in the working population attended college, there is a 0.94 probability the person is currently employed. If a person did not attend college, there is a 0.89 probability the person is currently employed. What is the probability a person did not attend college if the person is not currently employed

Answer 1

The probability that a person did not attend college if the person is not currently employed is 0.5602.

Explanation:

Denote the events as follows:

X = a person attended college

Y = a person is employed.

Given:

`P(X)=0.59\\P(Y|X)=0.94\\P(Y|X^(c))=0.89`

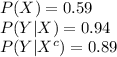
Compute the value of
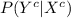`P(Y^(c)|X^(c))` as follows:

`P(Y^(c)|X^(c))=1-P(Y|X^(c)) = 1 - 0.89=0.11`

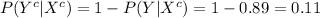
Compute the probability of a person being employed as follows:

`P(Y)=P(Y|X)P(X)+P(Y|X^(c))P(X^(c))\\=(0.94*0.59)+(0.89*(1-0.59))\\=0.5546+0.3649\\=0.9195`

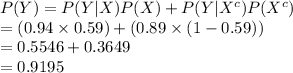
Then the value a person being not employed is:

`P(Y^(c))=1-P(Y)=1-0.9195=0.0805`

Compute the value of
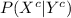`P(X^(c)|Y^(c))` as follows:

`P(X^(c)|Y^(c))=(P(Y^(c)|X^(c))P(X^(c)))/(P(Y^(c)))=(0.11*(1-0.59))/(0.0805)=0.5602`

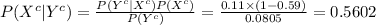
Thus, the probability that a person did not attend college if the person is not currently employed is 0.5602.