Answer:
1. Future value (FV) = $4,717
2. Future value (FV) = $5,189
3. Future value (FV) = $5,237
Step-by-step explanation:
Requirement 1
Assume that the present value of the investment is $1,000.
We know, Compounding yearly,
FV = PV*(1 + i)^n
Given,
Present value (PV) = $1,000
Interest rate, i = 13.8% = 0.138
number of periods, n = 12 years
We have to calculate the future value of the investment.
Therefore,
FV = $1,000 ×
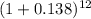
or, FV = $1,000 ×
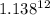
or, FV = $1,000 × 4.7174
Therefore, Future value (FV) = $4,717
Requirement 2
Again, Assume that the present value of the investment is $1,000.
We know, Compounding monthly,
FV = PV ×
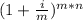
Given,
Present value (PV) = $1,000
Interest rate, i = 13.8% = 0.138
number of periods, n = 12 years
compounding period (monthly), m = 12
We have to calculate the future value of the investment.
Therefore,
FV = $1,000 ×
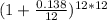
or, FV = $1,000 ×

or, FV = $1,000 ×
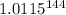
or, FV = $1,000 × 5.1890
Therefore, Future value (FV) = $5,189
Requirement 3
Again, Assume that the present value of the investment is $1,000.
We know, Compounding daily,
FV = PV ×
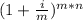
Given,
Present value (PV) = $1,000
Interest rate, i = 13.8% = 0.138
number of periods, n = 12 years
compounding period (daily), m = 365
We have to calculate the future value of the investment.
Therefore,
FV = $1,000 ×
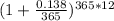
or, FV = $1,000 ×
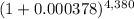
or, FV = $1,000 ×
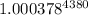
or, FV = $1,000 × 5.2367
Therefore, Future value (FV) = $5,237