Answer:
C) 7.35*10⁶ N/C radially outward
Step-by-step explanation:
- If we apply the Gauss'law, to a spherical gaussian surface with radius r=7 cm, due to the symmetry, the electric field must be normal to the surface, and equal at all points along it.
- So, we can write the following equation:

- As the electric field must be zero inside the conducting spherical shell, this means that the charge enclosed by a spherical gaussian surface of a radius between 4 and 5 cm, must be zero too.
- So, the +8 μC charge of the solid conducting sphere of radius 2cm, must be compensated by an equal and opposite charge on the inner surface of the conducting shell of total charge -4 μC.
- So, on the outer surface of the shell there must be a charge that be the difference between them:
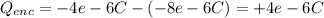
- Replacing in (1) A = 4*π*ε₀, and Qenc = +4 μC, we can find the value of E, as follows:
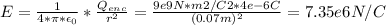
- As the charge that produces this electric field is positive, and the electric field has the same direction as the one taken by a positive test charge under the influence of this field, the direction of the field is radially outward, away from the positive charge.