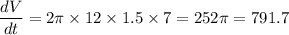Answer:
252π or 791.7 mm³/h
Explanation:
The volume of a cylinder is given by

We desire to find the volume rate, that is,
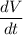
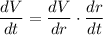
dr/dt is the rate of change of the radius which is 7 mm/h.
dV/dr is derived by differentiating the volume equation, yielding
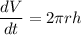
At r = 12 mm and h = 1.5 mm,