Question

A turbine blade made of a metal alloy (k = 17 W/m·K) has a length of 5.3 cm, a perimeter of 11 cm, and a cross-sectional area of 5.13 cm2. The turbine blade is exposed to hot gas from the combustion chamber at 1053°C with a convection heat transfer coefficient of 538 W/m2·K. The base of the turbine blade maintains a constant temperature of 450°C and the tip is adiabatic.

Answer 1

The base of the turbine blade maintains a constant temperature of 450°C and the tip is adiabatic is 1076.67° C.

Step-by-step explanation:

The rate of heat transfer for the turbine blade is expressed.

`Q=√(h P k A)\left(T_(b)-T_(\infty)\right) \tanh (m L)`

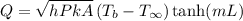
The parameters are calculated.

`m=\sqrt{(h P)/(k A)}`

`=\sqrt{\frac{\left(538 \mathrm{W} / \mathrm{m}^(2) \mathrm{K}\right)(0.11 \mathrm{m})}{(17 \mathrm{W} / \mathrm{m} \cdot \mathrm{K})\left(0.000513 \mathrm{m}^(2)\right)}}`

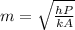
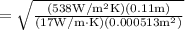
m = 82.38

Hence the rate of heat transfer for the turbine blade is

Q =
`√((538)(0.11)(17)(0.000513)(450-1093)tanh(82.38)(0.053))`

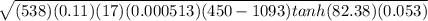
Q = -461.758 W

The temperature at the blade tip is calculated.

`(T_(x)-T_(\infty))/(T_(b)-T_(\infty))` =
`(1)/(\cosh (m L))`

`\frac{T_(x)-1093^(\circ) \mathrm{C}}{450^(\circ) \mathrm{C}-1093^(\circ) \mathrm{C}}` =
`(1)/(\cosh (82.38 * 0.053))`

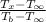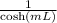
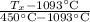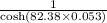
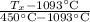`\frac{T_(x)-1093^(\circ) \mathrm{C}}{450^(\circ) \mathrm{C}-1093^(\circ) \mathrm{C}}` = 0.0254

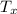`T_(x)` = 1076.67° C