Answer:
(a) P(X > $31,000) = 0.0427
(b) P($26,000 < X < $30,000) = 0.8005
(c) P(X < $25,000) = 0.0113
Explanation:
We are given that according to an annual survey conducted by a particular website, the mean cost of a wedding in 2012 was $28,423. Suppose the cost for a wedding is normally distributed, with a standard deviation of $1,500, and a wedding is selected at random.
Let X = cost for a wedding
So, X ~ N(
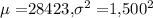 )
)
The z score probability distribution is given by;
Z =
 ~ N(0,1)
~ N(0,1)
(a) Probability that the wedding costs more than $31,000 = P(X>$31,000)
P(X > 31,000) = P(
 >
>
 ) = P(Z > 1.72) = 1 - P(Z <= 1.72)
) = P(Z > 1.72) = 1 - P(Z <= 1.72)
= 1 - 0.95728 = 0.0427
(b) Probability that the wedding costs between $26,000 and $30,000 = P($26,000 < X < $30,000) = P(X < $30,000) - P(X <= $26,000) \
P(X < 30,000) = P(
 <
<
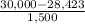 ) = P(Z < 1.05) = 0.85314
) = P(Z < 1.05) = 0.85314
P(X <= 26,000) = P(
 <=
<=
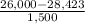 ) = P(Z <= -1.62) = 1 - P(Z <= 1.62)
) = P(Z <= -1.62) = 1 - P(Z <= 1.62)
= 1 - 0.94738 = 0.05262
Therefore, P($26,000 < X < $30,000) = 0.85314 - 0.05262 = 0.8005 .
(c) Probability that the wedding costs less than $25,000 = P(X < $25,000)
P(X < 25,000) = P(
 <
<
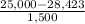 ) = P(Z < -2.28) = 1 - P(Z <= 2.28)
) = P(Z < -2.28) = 1 - P(Z <= 2.28)
= 1 - 0.98870 = 0.0113