Answer:
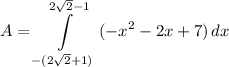
General Formulas and Concepts:
Calculus
Integration
Area of a Region Formula:
![\displaystyle A = \int\limits^b_a {[f(x) - g(x)]} \, dx](https://img.qammunity.org/2021/formulas/mathematics/college/8yomppr4m10wil0api6m0lag5b7hnc5c9y.png)
Explanation:
Step 1: Define
Identify
y = -x² + 4
y = 2x - 3
Step 2: Identify
Graph functions and find region and bounds of integration.
Bounds: [-(2√2 + 1), 2√2 - 1]
Step 3: Find Area
- Substitute in variables [Area of a Region Formula]:
![\displaystyle A = \int\limits^(2√(2) - 1)_(-(2√(2) + 1)) {[-x^2 + 4 - (2x - 3)]} \, dx](https://img.qammunity.org/2021/formulas/mathematics/middle-school/qxp9mlq600mklc85sbgj77g6on9568kcdf.png)
- Simplify:
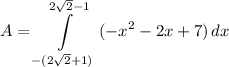
Topic: AP Calculus AB/BC (Calculus I/I + II)
Unit: Integration