Question

A 0.19-m3 rigid tank equipped with a pressure regulator contains steam at 2 MPa and 300°C. The steam in the tank is now heated. The regulator keeps the steam pressure constant by letting out some steam, but the temperature inside rises. Determine the amount of heat transferred when the steam temperature reaches 500°C. The properties of water are v1 = 0.12551 m3/kg, u1 = 2773.2 kJ/kg, h1 = 3024.2 kJ/kg, v2 = 0.17568 m3/kg, u2 = 3116.9 kJ/kg, and h2 = 3468.3 kJ/kg.

Answer 1

576.21kJ

Step-by-step explanation:

#We know that:

The balance mass
`m_(in)+m_(out)=\bigtriangleup m_(system)`

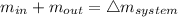
so,
`m_e=m_1-m_2`

`Energy \ Balance\\E_(in)-E_(out)=\bigtriangleup E_(system)\\\\\therefore Q_i_n+m_eh_e=m_2u_2-m_1u_1`

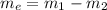
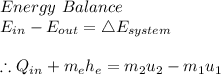
#Also, given the properties of water as;

`(P_1=2Mpa,T_1=300\textdegree C)->v_1=0.12551m^3/kg,u_1=2773.2kJ/kg->h_1=3024.2kJ/kg\\\\(P_2=2Mpa,T_1=500\textdegree C)->v_2=0.17568m^3/kg,u_1=3116.9kJ/kg->h_1=3468.3kJ/kg`

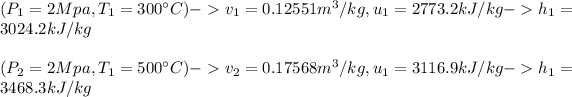
#We assume constant properties for the steam at average temperatures:
`h_e=\approx(h_1+h_2)/2`

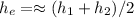
#Replace known values in the equation above;
`h_e=(3024.2+3468.3)/2=3246.25kJ/kg\\\\m_1=V_1/v_1=0.19m^3/(0.12551m^3/kg)=1.5138kg\\\\m_2=V_2/v_2=0.19m^3/(0.17568m^3/kg)=1.0815kg`

#Using the mass and energy balance relations;

`m_e=m_1-m_2\\\\m_e=1.5138-1.0815\\\\m_e=0.4323kg`

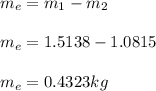
#We have
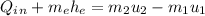`Q_i_n+m_eh_e=m_2u_2-m_1u_1`: we replace the known values in the equation as;

`Q_i_n+m_eh_e=m_2u_2-m_1u_1\\\\Q_i_n=0.4323kg*3246.2kJ/kg+1.0815kg*3116.9-1.5138kg*2773.2kJ/kg\\\\Q_i_n=573.21kJ`

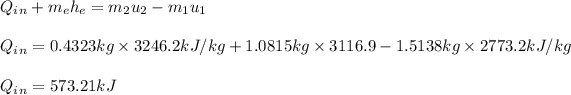
#Hence,the amount of heat transferred when the steam temperature reaches 500°C is 576.21kJ