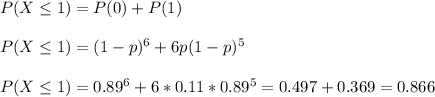Answer:
The probability that more than 6 samples are needed to have 2 mutations is P=0.866.
Explanation:
This question can be analized with the binomial distribution.
We need to calculate the probability that more of 6 samples are needed to have 2 samples with mutations.
This is equal to the proability of taking 2 samples and getting one mutation or less.
Then we have a binomial distribution with n=6 and p=0.11: