Answer:
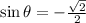 and
and

Explanation:
Given :
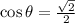 and
and
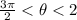
To find : Evaluate
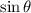 and
and
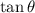 ?
?
Solution :
As
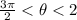 means
means
 belong to the third or fourth quadrant .
belong to the third or fourth quadrant .
So,
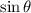 is negative and
is negative and
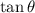 is positive in third and negative in fourth.
is positive in third and negative in fourth.
Using the formula of trigonometric,
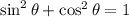
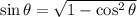
Substitute
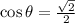 ,
,
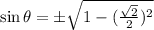
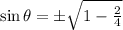
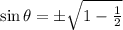
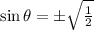
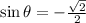
Now using another formula,
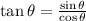
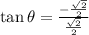

Therefore,
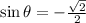 and
and
 .
.