Question

The population mean and standard deviation are given below. Find the indicated probability and determine whether a sample mean in the given range below would be considered unusual. If​ convenient, use technology to find the probability. For a sample of nequals36​, find the probability of a sample mean being less than 12 comma 750 or greater than 12 comma 753 when muequals12 comma 750 and sigmaequals1.7.

Answer 1

The sample mean would not be considered unusual because the probability is greater than or equal to 0.50 of the sample mean being within the range.

Explanation:

We are given the following information in the question:

Mean, μ = 12750

Standard Deviation, σ = 1.7

Sample size, n = 36

Formula:

`z_(score) = \displaystyle(x-\mu)/(\sigma)`

Standard error due to sampling:

`(\sigma)/(√(n)) = (1.7)/(√(36)) = 0.283`

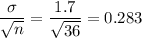
P(sample mean being less than 12,750 or greater than 12,753)

`1 - P( 12750 < x < 12753) = 1-P(\displaystyle(12750 - 12750)/(0.283) \leq z \leq \displaystyle(12753-12750)/(0.283))\\\\ = 1-(P(0 \leq z \leq 10.06))\\\\= 1-P(z \leq 10.06) +P(z < 0)\\= 1 - 1 + 0.500 = 0.500`

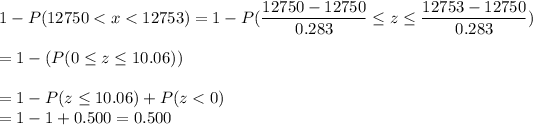
Thus, the sample mean would not be considered unusual because the probability is greater than or equal to 0.50 of the sample mean being within the range.