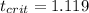Answer:
a) "=T.INV(1-0.02,7)"
And we got
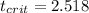
b) "=T.INV(0.85,7)"
And we got
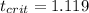
Explanation:
For this case we have a sample size of n=8, so we can find the degrees of freedom like this:
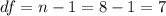
Part a
For this case we need a value who accumulates 0.02 of the area in the right of the t distribution with 7 degrees of freedom so we can use the following excel code:
"=T.INV(1-0.02,7)"
And we got
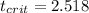
Part b
For this case we need a value who accumulates 0.85 of the area in the left of the t distribution with 7 degrees of freedom so we can use the following excel code:
"=T.INV(0.85,7)"
And we got