Question

Suppose that the amount of time T a customer spends in a bank is exponentially distributed with an average of 10 minutes. What is the probability that a customer will spend more than 15 minutes total in the bank, given that the customer has already waited over 10 minutes

Answer 1

The probability that a customer will spend more than 15 minutes total in the bank, given that the customer has already waited over 10 minutes is 0.6065.

Explanation:

The random variable T is defined as the amount of time a customer spends in a bank.

The random variable T is exponentially distributed.

The probability density function of a an exponential random variable is:

`f(x)=\lambda e^(-\lambda x);\ x>0`

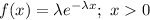
The average time a customer spends in a bank is β = 10 minutes.

Then the parameter of the distribution is:

`\lambda=(1)/(\beta)=(1)/(10)=0.10`

An exponential distribution has a memory-less property, i.e the future probabilities are not affected by any past data.

That is, P (X > s + x | X > s) = P (X > x)

So the probability that a customer will spend more than 15 minutes total in the bank, given that the customer has already waited over 10 minutes is:

P (X > 15 | X > 10) = P (X > 5)

`\int\limits^(\infty)_(5) {f(x)} \, dx =\int\limits^(\infty)_(5) {\lambda e^(-\lambda x)} \, dx\\=\int\limits^(\infty)_(5) {0.10 e^(-0.10 x)} \, dx\\=0.10\int\limits^(\infty)_(5) {e^(-0.10 x)} \, dx\\=0.10|(e^(-0.10 x))/(-0.10)|^(\infty)_(5)\\=[-e^(-0.10 * \infty)+e^(-0.10 * 5)]\\=0.6065`

Thus, the probability that a customer will spend more than 15 minutes total in the bank, given that the customer has already waited over 10 minutes is 0.6065.