Answer:
1.0042:1 is the ratio of the root mean square speed of
 to that of
to that of
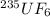 at constant temperature.
at constant temperature.
Step-by-step explanation:
The formula used for root mean square speed is:
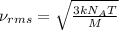
where,
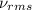 = root mean square speed
= root mean square speed
k = Boltzmann’s constant =
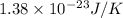
T = temperature = 370 K
M = atomic mass = 0.02 kg/mole
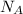 = Avogadro’s number =
= Avogadro’s number =
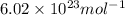
Root mean square speed of
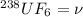
Molar mass of
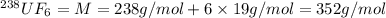
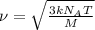
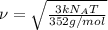 ..[1]
..[1]
Root mean square speed of

Molar mass of
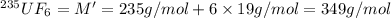
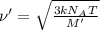
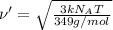 ..[2]
..[2]
[1] ÷ [2]

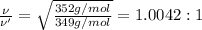
1.0042:1 is the ratio of the root mean square speed of
 to that of
to that of
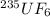 at constant temperature.
at constant temperature.