Question

For what value of x is the double product of the binomials x+2 and x–2 is 16 less than the sum of their squares?

pls help I’m confused

Answer 1

for all values of x = 2 is the double product of the binomials x+2 and x–2 is 16 less than the sum of their squares

Explanation:

By Using the difference of two square:

The product of the binomials:

`(x+2)(x-2)=(x^2-4)`

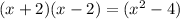
Double the product yields =
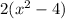`2(x^2-4)` ----- equation (1)

However, the sum of their squares can be expressed as follows:

`(x+2)^2+(x-2)^2`

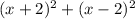
16 less than that will be:

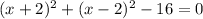`(x+2)^2+(x-2)^2-16=0` ----------- equation (2)

NOW; the question says for what value of the "x" are those two equation equal to each other;

To tackle the problem; we equate equation (1) and equation (2) together.

So; now we can have:

`2(x^2-4)` =
`(x+2)^2+(x-2)^2-16`

`2(x^2-4) = (x^2+2x+2x+4)+(x^2-2x-2x+4)-16`

`2x^2-8 = (x^2+4x+4)+(x^2-4x+4)-16`

`2x^2-8 = 2x^2+8-16`

`2x^2-8 = 2x^2-8`

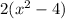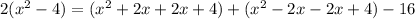
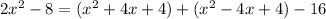
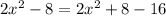
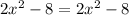
In this scenario; we found out that the left-hand side is equal to the right-hand side.

So;

`2x^2-8 = 0\\2x^2=8\\x^2 =(8)/(2) \\x^2 = 4\\x =√(4) \\x=2`

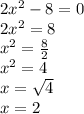
We therefore conclude that for all values of x = 2 is the double product of the binomials x+2 and x–2 is 16 less than the sum of their squares

Also, we can say that for all values of "x" =
`( \infty, + \infty)` for all intervals or
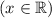`(x\in \mathbb{R})` for set notations.