Question

Suppose that a subatomic particle that normally decays in 18 nanoseconds is produced in a particle accelerator while traveling at a speed very close to the speed of light. The particle will then decay after ________.

Answer 1

The observer would see that the subatomic particle decays after 1800 ns.

Step-by-step explanation:

This would be more than 18 nanoseconds. When objects are traveling at the speed of light, their lifetime is longer to an observer. On the other hand, if you took the perspective of the subatomic particle, it would decay in 18 nanoseconds.

The value of time dilation is given as

`t'=\frac{t}{\sqrt{1-((v)/(c))^2}}`

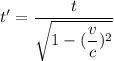
As the value of v is given such that it is close the c so assuming v=0.99c so v/c is 0.99 so

`t'=(t)/(√(1-(0.99)^2))\\t'=(18)/(√(1-(0.99)^2))\\t'=1800 ns`

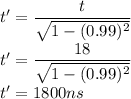
So the observer would see that the subatomic particle decays after 1800 ns.