Answer:
Speed during first part of the trip = 50 miles/hour
Speed during second part of trip = 53 miles/hour
Explanation:
Given:
Distance driven in rainstorm = 250 miles
Distance driven after rain stopped = 159 miles
Speed driven after rain stopped is 3 miles faster than the speed driven in rainstorm.
Total time driven = 8 hours
To find the speed of the car at each part of the trip.
Solution:
There are two parts of the trip.
1) Car driven in rainstorm:
Let the speed of the car during this part in miles/hour be =

Distance covered in this part = 250 miles.
Time taken in this trip =
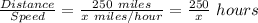
2) Car driven after rain stopped:
Speed of the car during this part in miles/hour will be =
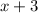
Distance covered in this part = 159 miles.
Time taken in this trip =
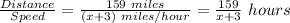
Total time driven can be given as:
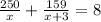
Solving for
 .
.
Taking LCD.
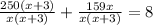
Simplifying.
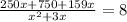
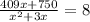
Multiplying both sides by
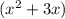
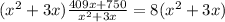
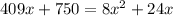
Subtracting both sides by 750.
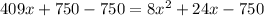
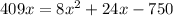
Subtracting both sides by

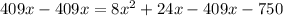
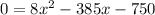
Applying quadratic formula.
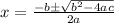
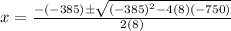

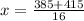 and
and
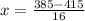
∴
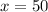 and
and
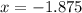
Since speed cannot be taken as negative, so our solution will be 50 miles per hour.
Speed during first part of the trip = 50 miles/hour
Speed during second part of trip =
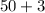 = 53 miles/hour
= 53 miles/hour