2 Answers

Terje Dahl · Answer 1 · 2021-08-23T13:40:11+0000

Answer:

20% probability of being in honors science if you are in honors math

Explanation:

I am going to say that we have two events.

Event A: Being in honors in math. So P(A) = 0.3.

Event B: Being in honors in science. So P(B) = 0.2.

Since they are independent events, we can apply the conditional probability formula, which is:

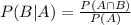
$P(B|A) = (P(A \cap B))/(P(A))$

In which

P(B|A) is the probabilitty of event B happening given that A happened. We want to find this.

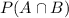$P(A \cap B)$ is the probability of both events happening.

Since they are independent

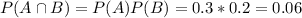
$P(A \cap B) = P(A)P(B) = 0.3*0.2 = 0.06$

So

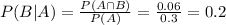
$P(B|A) = (P(A \cap B))/(P(A)) = (0.06)/(0.3) = 0.2$

20% probability of being in honors science if you are in honors math

Please log in or register to add a comment.