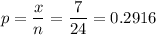Question

Data on oxide thickness of semiconductors are as follows: 426, 433, 415, 420, 420, 438, 417, 410, 430, 434, 423, 426, 412, 434, 435, 432, 409, 426, 409, 436, 422, 430, 411, 415.(a) Calculate a point estimate of the mean oxide thickness for all wafers in the population. (Round your answer to three decimal places.)(b) Calculate a point estimate of the standard deviation of oxide thickness for all wafers in the population. (Round your answer to two decimal places.)(c) Calculate the standard error of the point estimate from part (a). (Round your answer to two decimal places.)(d) Calculate a point estimate of the median oxide thickness for all wafers in the population. (Express your answer to one decimal places.)(e) Calculate a point estimate of the proportion of wafers in the population that have oxide thickness greater than 430 angstrom. (Round your answer to four decimal places.)

Answer 1

a) 423.458

b) 9.53

c) 1.94

d) 424.5

e) 0.2916

Explanation:

We are given the following in the question:

426, 433, 415, 420, 420, 438, 417, 410, 430, 434, 423, 426, 412, 434, 435, 432, 409, 426, 409, 436, 422, 430, 411, 415

a) point estimate of the mean oxide thickness

`Mean = \displaystyle\frac{\text{Sum of all observations}}{\text{Total number of observation}}`

`Mean =\displaystyle(10163)/(24) = 423.458`

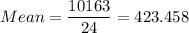
b) point estimate of the standard deviation of oxide thickness

`\text{Standard Deviation} = \sqrt{\displaystyle\frac{\sum (x_i -\bar{x})^2}{n-1}}`

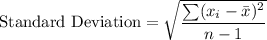
where
`x_i` are data points,
`\bar{x}` is the mean and n is the number of observations.

Sum of squares of differences = 2089.958

`s = \sqrt{(2089.958)/(23)} = 9.53`

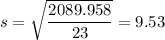
c) standard error of the point estimate

Standard error =

`=(\sigma)/(√(n)) = (9.53)/(√(24)) = 1.94`

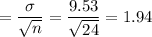
d) point estimate of the median oxide thickness

Sorted data: 409, 409, 410, 411, 412, 415, 415, 417, 420, 420, 422, 423, 426, 426, 426, 430, 430, 432, 433, 434, 434, 435, 436, 438

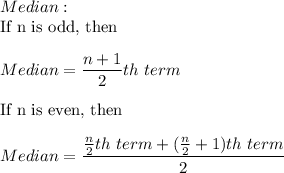
`Median:\\\text{If n is odd, then}\\\\Median = \displaystyle(n+1)/(2)th ~term \\\\\text{If n is even, then}\\\\Median = \displaystyle((n)/(2)th~term + ((n)/(2)+1)th~term)/(2)`

Median =

`(12^(th)+13^(th))/(2) = (423+426)/(2) = 424.5`

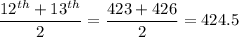
e) proportion of wafers in the population that have oxide thickness greater than 430 angstrom

Sample size, n = 24

Number of wafers with oxides greater than 430 angstrom, x = 7

`p = (x)/(n) = (7)/(24) = 0.2916`