Question

HELP NEEDED IMMEDIATELY! I'M GETTING DESPERATE!

For an integer $n$, the inequality

\[x^2 + nx + 15 < 0\]has no real solutions in $x$. Find the number of different possible values of $n$.

Answer 1

The number of different possible values are {-7,-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6,7}.

Explanation:

Given : For an integer n, the inequality
`\[x^2 + nx + 15 < 0\]` has no real solutions in x.

To find : The number of different possible values of n ?

Solution :

The given inequality is
`\[x^2 + nx + 15 < 0\]` have no solution then the discriminant must be less than zero.

i.e.
`b^2-4ac<0`

Here, a=1, b=n and c=15

`{n}^(2) - 4 * 1 * 15 \: < \: 0`

`{n}^(2) - 60 \: < \: 0`

`n^2<60`

`n<\pm √(60)`

`n<\pm 7.75`

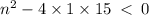
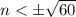
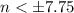
i.e.
`- 7.75 \: < \: n \: < \: 7.75`

The integer values are {-7,-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6,7}.