Question

The man (75 Kg) is climbing up the rope with acceleration 0.25 m/s2 relative to the rope. MA = 80 Kg. What is the rope tension and aA? Ans: aA = 0.195 m/s2 down, T = 769 N

Answer 1

a = 0.195 m/s²

T = 769.2 N

Step-by-step explanation:

The sum of the forces (ΣF) acting on the man climbing up the rope is:

`\sum F_(y) = m_(m)a_(m)`

`T - m_(m)g = ma_(m)`

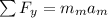
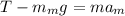
where
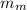`m_(m)`: is the mass of the man,
`a_(m)`: is the acceleration of the man, T: is the tension and g: is the gravitational constant

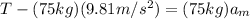`T - (75 kg)(9.81 m/s^(2)) = (75 kg)a_(m)` (1)

Since the acceleration of the man is relative to the rope, the acceleration of the man is:

`a_(r) = a_(m) - a`

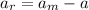
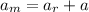`a_(m) = a_(r) + a` (2)

where
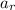`a_(r)`: is the acceleration of the man relative to the rope and a: is the acceleration of the rope = acceleration of the block A

By introducing equation (2) into (1) we have:

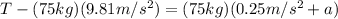`T - (75 kg)(9.81 m/s^(2)) = (75 kg)(0.25 m/s^(2) + a)` (3)

The sum of the forces acting on the block A is:

`\sum F_(y) = ma`

`m_(b)g - T = ma`

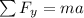
where
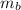`m_(b)`: is the mass of the block A

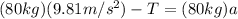`(80 kg)(9.81 m/s^(2)) - T = (80 kg)a` (4)

Now, solving equations (3) and (4) for a and T, we have:

`a = (g(m_(b) - m_(m)) - (0.25)(m_(m)))/(m_(b) + m_(m))`

`a = (9.81 m/s^(2)( 80 kg- 75 kg) - (0.25 m/s^(2))(75 kg))/(80 kg + 75 kg) = 0.195 m/s^(2)`

`T = m_(b)g - m_(b)a = (80 kg)(9.81 m/s^(2)) - (80 kg)(0.195 m/s^(2)) = 769.2 N`

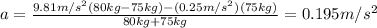
I hope it helps you!