Question

While on the moon, the Apollo astronauts enjoyed the effects of a gravity much smaller than that on Earth. If Neil Armstrong jumped up on the moon with an initial speed of 1.51 m/s to a height of 0.700 m, what amount of gravitational acceleration did he experience?

Answer 1

The gravitational acceleration experienced was of 1.63m/s².

Step-by-step explanation:

We know, from the kinematics equations of vertical motion that:

`v^(2) =v_0^2-2gy`

Solving for g, we get:

`g=-(v^2-v_0^2)/(2y)`

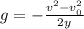
Since the final speed is zero, because Neil Armstrong came to a stop in his maximum height, we obtain:

`g=(v_0^2)/(2y)`

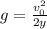
Finally, we plug in the given values of the initial speed and the maximum height:

`g=((1.51m/s)^2)/(2(0.700m))=1.63m/s^2`

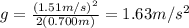
This means that the gravitational acceleration experienced by Neil Armstrong in the moon, was of 1.63m/s².