Question

An unstretched spring has a length of 10. centimeters. When the spring is stretched by a force of 16 newtons, its length is increased to 18 centimeters. What is the spring constant of this spring

Answer 1

The spring constant of this spring is 200 N/m.

Step-by-step explanation:

Given:

Original unstretched length of the spring (x₀) = 10 cm =0.10 m [1 cm =0.01 m]

Stretched length of the spring (x₁) = 18 cm = 0.18 cm

Force acting on the spring (F) = 16 N

Spring constant of the spring (k) = ?

First let us find the change in length of the spring or the elongation caused in the spring due to the applied force.

So, Change in length = Final length - Initial length

`\Delta x = x_1-x_0=0.18-0.10=0.08\ m`

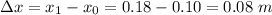
Now, restoring force acting on the spring is directly related to its elongation or compression as:

`F=k\Delta x`

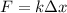
Rewriting in terms of 'k', we get:

`k=(F)/(\Delta x)`

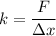
Now, plug in the given values and solve for 'k'. This gives,

`k=(16\ N)/(0.08\ m)\\\\k=200\ N/m`

Therefore, the spring constant of this spring is 200 N/m.